Forecasting Time Series - In Depth

This tutorial provides an in-depth overview of the time series forecasting capabilities in AutoGluon. Specifically, we will cover:

• What is probabilistic time series forecasting?

• Forecasting time series with additional information

• Which forecasting models are available in AutoGluon?

• How does AutoGluon evaluate performance of time series models?

• What functionality does TimeSeriesPredictor offer?

  • Basic configuration with presets and time_limit

  • Manually selecting what models to train

  • Hyperparameter tuning

  • Forecasting irregularly-sampled time series

This tutorial assumes that you are familiar with the contents of Forecasting Time Series - Quick Start.

What is probabilistic time series forecasting?

A time series is a sequence of measurements made at regular intervals. The main objective of time series forecasting is to predict the future values of a time series given the past observations. A typical example of this task is demand forecasting. For example, we can represent the number of daily purchases of a certain product as a time series. The goal in this case could be predicting the demand for each of the next 14 days (i.e., the forecast horizon) given the historical purchase data. In AutoGluon, the prediction_length argument of the TimeSeriesPredictor determines the length of the forecast horizon.

Fig. 5 Main goal of forecasting is to predict the future values of a time series given the past observations.

The objective of forecasting could be to predict future averages of a given time series, as well as establishing prediction intervals within which the future values will likely lie. In AutoGluon, the TimeSeriesPredictor generates two types of forecasts:

• mean forecast represents the expected value of the time series at each time step in the forecast horizon.

• quantile forecast represents the quantiles of the forecast distribution. For example, if the 0.1 quantile (also known as P10, or the 10th percentile) is equal to x, it means that the time series value is predicted to be below x 10% of the time. As another example, the 0.5 quantile (P50) corresponds to the median forecast. Quantiles can be used to reason about the range of possible outcomes. For instance, by the definition of the quantiles, the time series is predicted to be between the P10 and P90 values with 80% probability.

Fig. 6 Mean and quantile (P10 and P90) forecasts.

By default, the TimeSeriesPredictor outputs the quantiles [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]. Custom quantiles can be provided with the quantile_levels argument

predictor = TimeSeriesPredictor(quantile_levels=[0.05, 0.5, 0.95])

Forecasting time series with additional information

In real-world forecasting problems we often have access to additional information, beyond just the raw time series values. AutoGluon supports two types of such additional information: static features and known covariates.

Static features

Static features are the time-independent attributes (metadata) of a time series. These may include information such as:

• location, where the time series was recorded (country, state, city)

• fixed properties of a product (brand name, color, size, weight)

• store ID or product ID

Providing this information may, for instance, help forecasting models generate similar demand forecasts for stores located in the same city.

In AutoGluon, static features are stored as an attribute of a TimeSeriesDataFrame object. As an example, let’s have a look at the M4 Daily dataset.

import pandas as pd
from autogluon.timeseries import TimeSeriesDataFrame, TimeSeriesPredictor

We download a subset of 100 time series and the related metadata, similar to the Quickstart tutorial (click on the arrow to show the preprocessing code).

Loader for M4 Daily dataset

pd.set_option('display.max_rows', 6)  # Save space when printing

M4_INFO_URL = "https://github.com/Mcompetitions/M4-methods/raw/master/Dataset/M4-info.csv"
M4_DAILY_URL = "https://github.com/Mcompetitions/M4-methods/raw/master/Dataset/Train/Daily-train.csv"

def download_m4_daily_dataset(save_path, metadata_save_path=None, num_items_to_load=100):
    metadata = pd.read_csv(M4_INFO_URL)
    metadata = metadata[metadata["SP"] == "Daily"].set_index("M4id")
    # Select a subset of time series for faster processing
    metadata = metadata.sample(num_items_to_load, random_state=42)
    if metadata_save_path is not None:
        metadata["Domain"] = metadata["category"]
        metadata[["Domain"]].to_csv(metadata_save_path)

    data = pd.read_csv(M4_DAILY_URL, index_col="V1")
    results = []
    for item_id in metadata.index:
        time_series = data.loc[item_id].dropna().values
        start_time = pd.Timestamp(metadata.loc[item_id]["StartingDate"])
        timestamps = pd.date_range(start_time, freq="D", periods=len(time_series))
        results.append(pd.DataFrame({"M4id": [item_id] * len(time_series), "Date": timestamps, "Value": time_series}))
    result = pd.concat(results, ignore_index=True)
    result.to_csv(save_path, index=False)

download_m4_daily_dataset(save_path="m4_daily.csv", metadata_save_path="m4_daily_metadata.csv")

We load the individual time series into a TimeSeriesDataFrame:

ts_dataframe = TimeSeriesDataFrame.from_data_frame(
    pd.read_csv("m4_daily.csv", parse_dates=["Date"]),
    id_column="M4id",
    timestamp_column="Date",
)
ts_dataframe

		Value
item_id	timestamp
D1737	1995-05-23 12:00:00	1900.0
	1995-05-24 12:00:00	1877.0
	1995-05-25 12:00:00	1873.0
...	...	...
D2345	2013-07-06 12:00:00	10285.4
	2013-07-07 12:00:00	10135.9
	2013-07-08 12:00:00	10201.5

244460 rows × 1 columns

AutoGluon expects static features as a pandas.DataFrame object, where the index column

• is called "item_id"

• includes all the item_ids present in the respective TimeSeriesDataFrame.

static_features = pd.read_csv("m4_daily_metadata.csv", index_col="M4id")
static_features.index.rename("item_id", inplace=True)
static_features

	Domain
item_id
D1737	Industry
D1843	Industry
D2246	Finance
...	...
D2321	Finance
D2104	Finance
D2345	Finance

100 rows × 1 columns

In the M4 Daily dataset, there is a single categorical static feature that denotes the domain of origin for each time series.

We attach the static features to a TimeSeriesDataFrame as follows

ts_dataframe.static_features = static_features

If static_features doesn’t contain some item_ids that are present in ts_dataframe, an exception will be raised.

Now, when we fit the predictor, all models that support static features will automatically use the static features included in ts_dataframe.

predictor = TimeSeriesPredictor(target="Value").fit(ts_dataframe)

During fitting, the predictor will log how each static feature was interpreted as follows:

...
Following types of static features have been inferred:
    categorical: ['Domain']
    continuous (float): []
...

This message confirms that columns 'Domain' was interpreted as a categorical feature. In general, AutoGluon-TimeSeries supports two types of static features:

• categorical: columns of dtype object, string and category are interpreted as discrete categories

• continuous: columns of dtype int and float are interpreted as continuous (real-valued) numbers

• columns with other dtypes are ignored

To override this logic, we need to manually change the columns dtype. For example, suppose the static features data frame contained an integer-valued column "store_id".

ts_dataframe.static_features["store_id"] = list(range(len(ts_dataframe)))

By default, this column will be interpreted as a continuous number. We can force AutoGluon to interpret it a a categorical feature by changing the dtype to category.

ts_dataframe.static_features["store_id"] = ts_dataframe.static_features["store_id"].astype("category")

Note: If training data contained static features, the predictor will expect that data passed to predictor.predict(), predictor.leaderboard(), and predictor.evaluate() also includes static features with the exact same column names and data types.

Known covariates

Covariates are the time-varying features that may influence the target time series. They are sometimes also referred to as dynamic features, exogenous regressors, or related time series. AutoGluon currently supports covariates that are known in advance for the forecast horizon. Examples of such covariates include:

• holidays

• day of the week, month, year

• promotions

• weather forecasts (available in the future via weather forecasts)

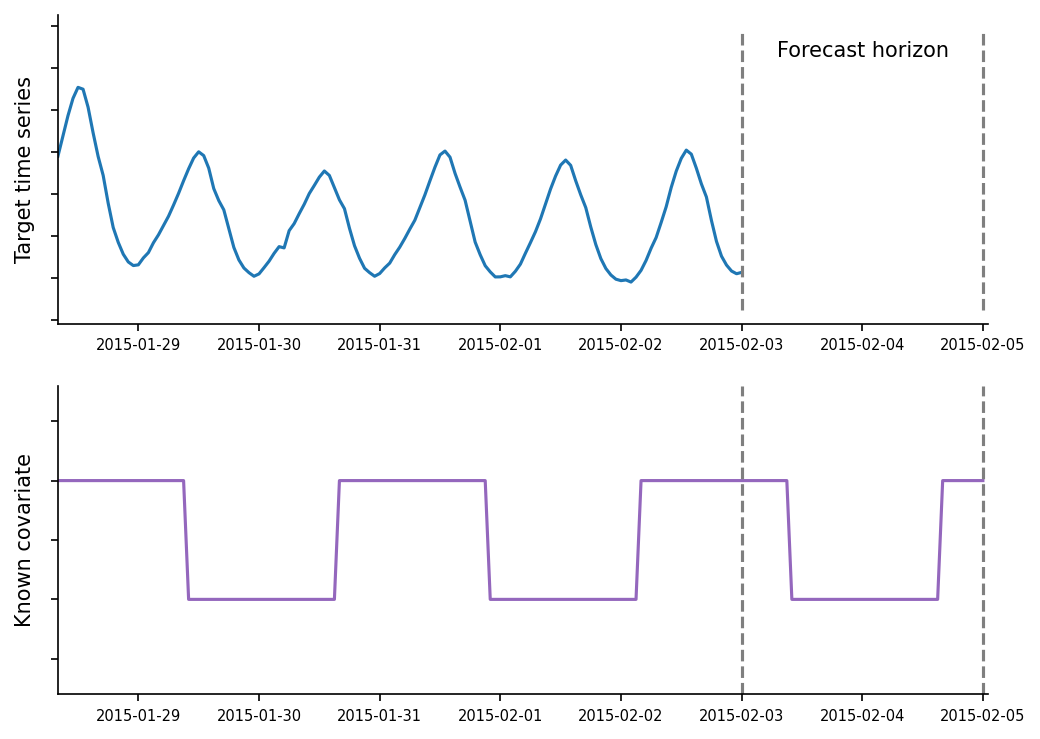
Fig. 7 Target time series with one known covariate.

As an example, we will again use the M4 Daily dataset.

prediction_length = 48
ts_dataframe = TimeSeriesDataFrame.from_data_frame(
    pd.read_csv("m4_daily.csv", parse_dates=["Date"]),
    id_column="M4id",
    timestamp_column="Date",
)
ts_dataframe

		Value
item_id	timestamp
D1737	1995-05-23 12:00:00	1900.0
	1995-05-24 12:00:00	1877.0
	1995-05-25 12:00:00	1873.0
...	...	...
D2345	2013-07-06 12:00:00	10285.4
	2013-07-07 12:00:00	10135.9
	2013-07-08 12:00:00	10201.5

244460 rows × 1 columns

In this example, we will generate a known covariate Weekend that equals to 1 if a given day is a weekend, and 0 otherwise. First, we generate the covariate for the training set.

WEEKEND_INDICES = [5, 6]
timestamps = ts_dataframe.index.get_level_values("timestamp")
ts_dataframe["Weekend"] = timestamps.weekday.isin(WEEKEND_INDICES).astype(float)
ts_dataframe

		Value	Weekend
item_id	timestamp
D1737	1995-05-23 12:00:00	1900.0	0.0
	1995-05-24 12:00:00	1877.0	0.0
	1995-05-25 12:00:00	1873.0	0.0
...	...	...	...
D2345	2013-07-06 12:00:00	10285.4	1.0
	2013-07-07 12:00:00	10135.9	1.0
	2013-07-08 12:00:00	10201.5	0.0

244460 rows × 2 columns

When creating the TimeSeriesPredictor, we specify that the column "Value" is our prediction target, and the column "Weekend" contains a covariate that will be known at prediction time.

predictor = TimeSeriesPredictor(
    prediction_length=prediction_length,
    target="Value",
    known_covariates_names=["Weekend"],
)
predictor.fit(ts_dataframe)

If the data frame contained additional columns (other than those specified in target and known_covariates_names), they would be ignored.

Next, to make predictions, we generate the known covariates for the forecast horizon

# Time difference between consecutive timesteps
offset = pd.tseries.frequencies.to_offset(ts_dataframe.freq)

known_covariates_per_item = []
for item_id in ts_dataframe.item_ids:
    time_series = ts_dataframe.loc[item_id]
    last_day = time_series.index[-1]
    future_timestamps = pd.date_range(start=last_day + offset, freq=offset, periods=prediction_length)
    weekend = future_timestamps.weekday.isin(WEEKEND_INDICES).astype(float)

    index = pd.MultiIndex.from_product([[item_id], future_timestamps], names=["item_id", "timestamp"])
    known_covariates_per_item.append(pd.DataFrame(weekend, index=index, columns=["Weekend"]))

known_covariates = TimeSeriesDataFrame(pd.concat(known_covariates_per_item))
known_covariates

		Weekend
item_id	timestamp
D1737	1997-05-28 12:00:00	0.0
	1997-05-29 12:00:00	0.0
	1997-05-30 12:00:00	0.0
...	...	...
D2345	2013-08-23 12:00:00	0.0
	2013-08-24 12:00:00	1.0
	2013-08-25 12:00:00	1.0

4800 rows × 1 columns

Note that known_covariates must satisfy the following conditions:

• The columns must include all columns listed in predictor.known_covariates_names

• The item_id index must include all item ids present in ts_dataframe

• The timestamp index must include the values for prediction_length many time steps into the future from the end of each time series in ts_dataframe

If known_covariates contain more information than necessary (e.g., contain additional columns, item_ids, or timestamps), AutoGluon will automatically select the necessary rows and columns.

Finally, we pass the known_covariates to the predict function to generate predictions

predictor.predict(ts_dataframe, known_covariates=known_covariates)

The list of models that support static features and covariates is available in Forecasting Time Series - Model Zoo.

Which forecasting models are available in AutoGluon?

Forecasting models in AutoGluon can be divided into three broad categories: local, global, and ensemble models.

Local models are simple statistical models that are specifically designed to capture patterns such as trend or seasonality. Despite their simplicity, these models often produce reasonable forecasts and serve as a strong baseline. Some examples of available local models:

• ETS

• ARIMA

• Theta

• SeasonalNaive

If the dataset consists of multiple time series, we fit a separate local model to each time series — hence the name “local”. This means, if we want to make a forecast for a new time series that wasn’t part of the training set, all local models will be fit from scratch for the new time series.

Global models are machine learning algorithms that learn a single model from the entire training set consisting of multiple time series. Most global models in AutoGluon are provided by the GluonTS library. These are neural-network algorithms (implemented in PyTorch or MXNet), such as:

• DeepAR

• SimpleFeedForward

• TemporalFusionTransformerMXNet

AutoGluon also offers a tree-based global model AutoGluonTabular. Under the hood, this model converts the forecasting task into a regression problem and uses a autogluon.tabular.TabularPredictor to fit gradient-boosted tree algorithms like XGBoost, CatBoost, and LightGBM.

Finally, an ensemble model works by combining predictions of all other models. By default, TimeSeriesPredictor always fits a WeightedEnsemble on top of other models. This can be disabled by setting enable_ensemble=False when calling the fit method.

For a list of tunable hyperparameters for each model, their default values, and other details see Forecasting Time Series - Model Zoo.

How does AutoGluon evaluate performance of time series models?

AutoGluon evaluates the performance of forecasting models by measuring how well their forecasts align with the actually observed time series. We can evaluate the performance of a trained predictor on test_data using the evaluate method

# Fit a predictor to training data
predictor = TimeSeriesPredictor(prediction_length=3, eval_metric="MAPE")
predictor.fit(train_data=train_data)
# Evaluate the predictor on test data
predictor.evaluate(test_data)

For each time series in test_data, the predictor does the following:

1. Hold out the last prediction_length values of the time series.

2. Generate a forecast for the held out part of the time series, i.e., the forecast horizon.

3. Quantify how well the forecast matches the actually observed (held out) values of the time series using the eval_metric.

Finally, the scores are averaged over all time series in the dataset.

The crucial detail here is that evaluate always computes the score on the last prediction_length time steps of each time series. The beginning of each time series (except the last prediction_length time steps) is only used to initialize the models before forecasting.

Multi-window backtesting

If we want to perform multi-window backtesting (i.e., evaluate performance on multiple forecast horizons generated from the same time series), we need to generate a new test set with multiple copies for each original time series. This can be done using a MultiWindowSplitter.

from autogluon.timeseries.spitter import MultiWindowSplitter

splitter = MultiWindowSplitter(num_windows=5)
_, test_data_multi_window = splitter.split(test_data, prediction_length)

predictor.evaluate(test_data_multi_window)

The new test set test_data_multi_window will now contain up to num_windows time series for each original time series in test_data. The score will be computed on the last prediction_length time steps of each time series (marked in orange).

Fig. 8 MultiWindowSplitter splits each original time series into multiple evaluation instances. Forecast is evaluated on the last prediction_length timesteps (orange).

Multi-window backtesting typically results in more accurate estimation of the forecast quality on unseen data. However, this strategy decreases the amount of training data available for fitting models, so we recommend using single-window backtesting if the training time series are short.

How to choose and interpret the evaluation metric?

Different evaluation metrics capture different properties of the forecast, and therefore depend on the application that the user has in mind. For example, weighted quantile loss ("mean_wQuantileLoss") measures how well-calibrated the quantile forecast is; mean absolute scaled error ("MASE") compares the mean forecast to the performance of a naive baseline. For more details about the available metrics, see the documentation for autogluon.timeseries.evaluator.TimeSeriesEvaluator.

Note that AutoGluon always reports all metrics in a higher-is-better format. For this purpose, some metrics are multiplied by -1. For example, if we set eval_metric="MASE", the predictor will actually report -MASE (i.e., MASE score multiplied by -1). This means the test_score will be between 0 (best possible forecast) and \(-\infty\) (worst possible forecast).

How does AutoGluon perform validation?

When we fit the predictor with predictor.fit(train_data=train_data), under the hood AutoGluon further splits the original dataset train_data into train and validation parts.

Performance of different models on the validation set is evaluated using the evaluate method, just like described above. The model that achieves the best validation score will be used for prediction in the end.

By default, the internal validation set uses the last prediction_length time steps of each time series (i.e., single-window backtesting). To use multi-window backtesting instead, set the validation_splitter argument to "multi_window"

# Defaults to 3 windows
predictor = TimeSeriesPredictor(..., validation_splitter="multi_window")

or pass a MultiWindowSplitter object

from autogluon.timeseries.splitter import MultiWindowSplitter

splitter = MultiWindowSplitter(num_windows=5)
predictor = TimeSeriesPredictor(..., validation_splitter=splitter)

Alternatively, a user can provide their own validation set to the fit method and forego using the splitter completely. In this case it’s important to remember that the validation score is computed on the last prediction_length time steps of each time series.

predictor = TimeSeriesPredictor(...)
predictor.fit(train_data=train_data, tuning_data=my_validation_dataset)

What functionality does TimeSeriesPredictor offer?

AutoGluon offers multiple ways to configure the behavior of a TimeSeriesPredictor that are suitable for both beginners and expert users.

Basic configuration with presets and time_limit

We can fit TimeSeriesPredictor with different pre-defined configurations using the presets argument of the fit method.

predictor = TimeSeriesPredictor(...)
predictor.fit(train_data, presets="medium_quality")

Higher quality presets usually result in better forecasts but take longer to train. The following presets are available:

• "fast_training": fit simple “local” statistical models (ETS, ARIMA, Theta, Naive, SeasonalNaive). These models are fast to train, but cannot capture more complex patters in the data.

• "medium_quality": all models in "fast_training" in addition to the tree-based AutoGluonTabular and the DeepAR deep learning model. Default setting that produces good forecasts with reasonable training time.

• "high_quality": all models in "medium_quality" in addition to two more deep learning models: TemporalFusionTransformerMXNet (if MXNet is available) and SimpleFeedForward. Moreover, this preset will enable hyperparameter optimization for local statistical models. Usually more accurate than medium_quality, but takes longer to train.

• "best_quality": all models in "high_quality" in addition to the transformer-based TransformerMXNet model (if MXNet is available). This setting also enables hyperparameter optimization for deep learning models. Usually better than high_quality, but takes much longer to train.

Another way to control the training time is using the time_limit argument.

predictor.fit(
    train_data,
    time_limit=60 * 60,  # total training time in seconds
)

If no time_limit is provided, the predictor will train until all models have been fit.

Manually configuring models

Advanced users can override the presets and manually specify what models should be trained by the predictor using the hyperparameters argument.

predictor = TimeSeriesPredictor(...)

predictor.fit(
    train_data,
    hyperparameters={
        "DeepAR": {},
        "ETS": {"seasonal_period": 7},
    }
)

The code above will only train two models:

• DeepAR (with default hyperparameters)

• ETS (with the given seasonal_period; all other parameters set to their defaults).

For the full list of available models and the respective hyperparameters, see Forecasting Time Series - Model Zoo.

Hyperparameter tuning

Advanced users can define search spaces for model hyperparameters and let AutoGluon automatically determine the best configuration for the model.

import autogluon.core as ag

predictor = TimeSeriesPredictor()

predictor.fit(
    train_data,
    hyperparameters={
        "DeepAR": {
            "hidden_size": ag.space.Int(20, 100),
            "dropout_rate": ag.space.Categorical(0.1, 0.3),
        },
    },
    hyperparameter_tune_kwargs="auto",
    enable_ensemble=False,
)

This code will train multiple versions of the DeepAR model with 10 different hyperparameter configurations. AutGluon will automatically select the best model configuration that achieves the highest validation score and use it for prediction.

AutoGluon uses different hyperparameter optimization (HPO) backends for different models:

• Ray Tune for GluonTS models implemented in MXNet (e.g., DeepARMXNet, TemporalFusionTransformerMXNet)

• Custom backend implementing random search for all other models

We can change the number of random search runs by passing a dictionary as hyperparameter_tune_kwargs

predictor.fit(
    ...
    hyperparameter_tune_kwargs={
        "scheduler": "local",
        "searcher": "random",
        "num_trials": 20,
    },
    ...
)

The hyperparameter_tune_kwargs dict must include the following keys:

• "num_trials": int, number of configurations to train for each tuned model

• "searcher": one of "random" (random search), "bayes" (bayesian optimization for GluonTS MXNet models, random search for other models) and "auto" (same as "bayes").

• "scheduler": the only supported option is "local" (all models trained on the same machine)

Note: HPO significantly increases the training time for most models, but often provides only modest performance gains.

Forecasting irregularly-sampled time series

By default, TimeSeriesPredictor expects the time series data to be regularly sampled (e.g., measurements done every day). However, in some applications, like finance, data often comes with irregular measurements (e.g., no stock price is available for weekends or holidays).

To train on such irregularly-sampled time series, we can set the ignore_time_index flag in the predictor.

predictor = TimeSeriesPredictor(..., ignore_time_index=True)
predictor.fit(train_data=train_data)

In this case, the predictor will completely ignore the timestamps in train_data, and the predictions made by the model will have a dummy timestamp index with frequency equal to 1 second. Also, the seasonality will be disabled for models like as ETS and ARIMA.